Sparse sets

A sparse set is a simple data structure that has a few interesting properties:

O(1) to add an item.
O(1) to remove an item.
O(1) to lookup an item.
O(1) to clear the set.
O(n) to iterate over the set.
A set does not require its internal items storage to be initialised upon creation (!).

Sparse sets are commonly used to implement Entity Component System architectural pattern. I plan to cover ECS in one of my future posts but for now let’s try to understand and implement sparse sets.

Overview

Sparse sets use two integer arrays internally: dense and sparse. The former is a packed array that stores the set’s items (integers) in the insertion order. The latter is an array that can have holes (hence the name – sparse) and it maps the set’s items to their indices in dense. The set also keeps track of how many items it has. We call it N.

Sparse sets could be implemented as growable, i.e. being able to reallocate the memory they use but I will use non-growable version in this post for simplicity. This means a user has to specify the size of the set upon creation.

/** An item stored in a sparse set. */
typedef uint32_t rho_ss_id;

/** Maximum possible value of the rho_ss_id. */
static const rho_ss_id rho_ss_id_max = UINT32_MAX - 1;

/** The sparse set. */
struct rho_ss {
    rho_ss_id *sparse;  /**< Sparse array used to speed-optimise the set.     */
    rho_ss_id *dense;   /**< Dense array that stores the set's items.         */
    rho_ss_id  n;       /**< Number of items in the dense array.              */
    rho_ss_id  max;     /**< Maximum allowed item ID.                         */
};

An empty set

We start with an empty set that can have up to max items. The next picture demonstrates the sparse set that can hold up to ten items.

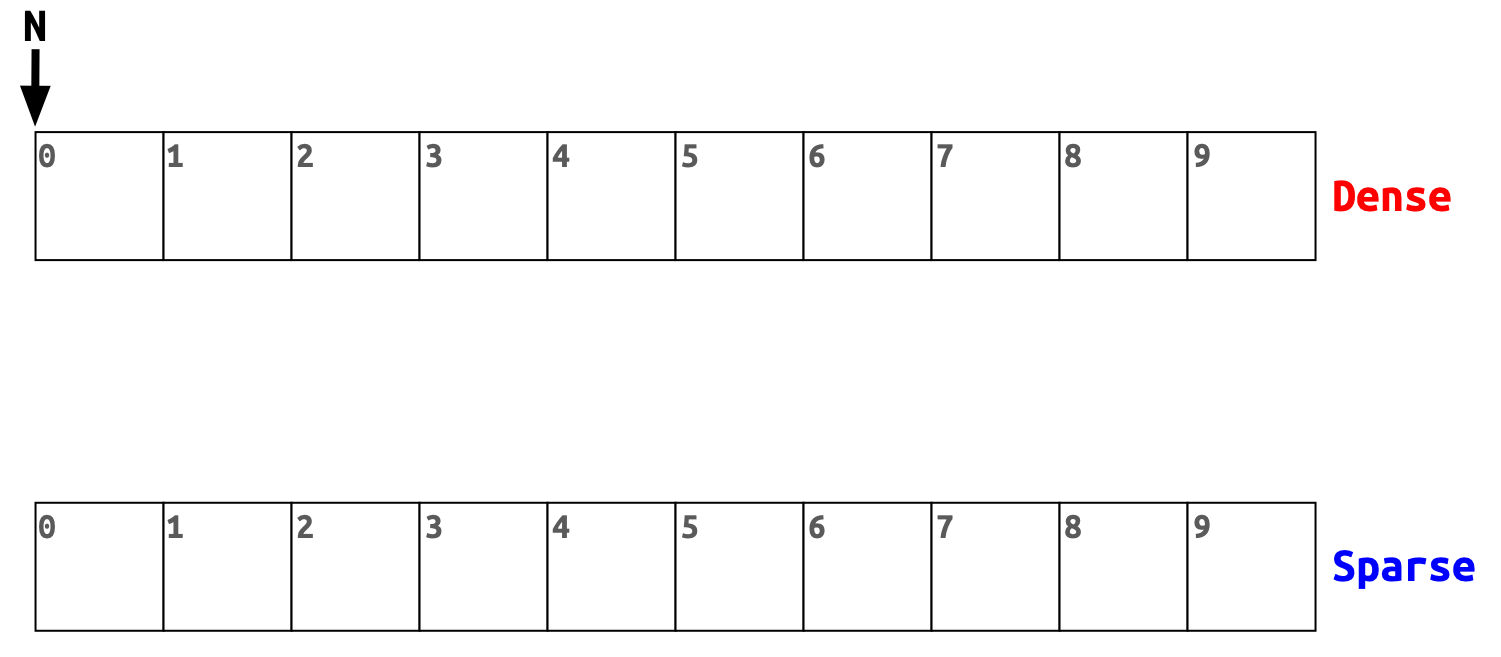
N is zero, dense and sparse are allocated but not initialised.

struct rho_ss rho_ss_alloc( rho_ss_id max_id )
{
    assert( max_id > 0 && max_id <= rho_ss_id_max );

    size_t        array_size = sizeof( rho_ss_id ) * ( max_id + 1 );
    struct rho_ss ss         = { 0 };

    ss.dense  = malloc( array_size );
    ss.sparse = malloc( array_size );

    if ( !ss.dense || !ss.sparse ) {
        free( ss.dense );
        free( ss.sparse );

        ss.dense  = NULL;
        ss.sparse = NULL;
    } else {
        ss.max = max_id;
    }

    return ss;
}

Adding a first item

Let’s add 4 as a first item to the set.

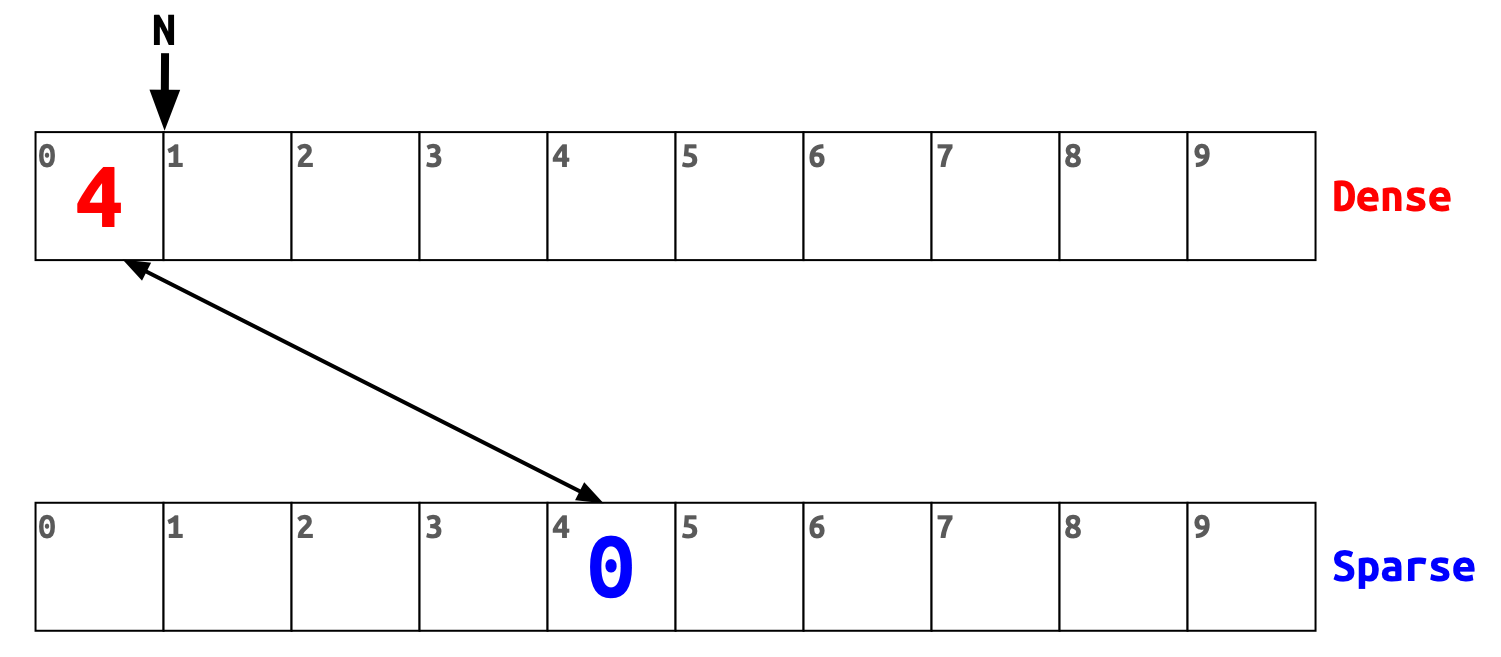
First, we add the item to the dense at index 0 (this is the current value of N). Then we write N to the sparse array at index 4. Now both slots in the dense and sparse arrays point to each other. Lastly, we increase N by one.

Adding a second item

Let’s add 6 as a second item.

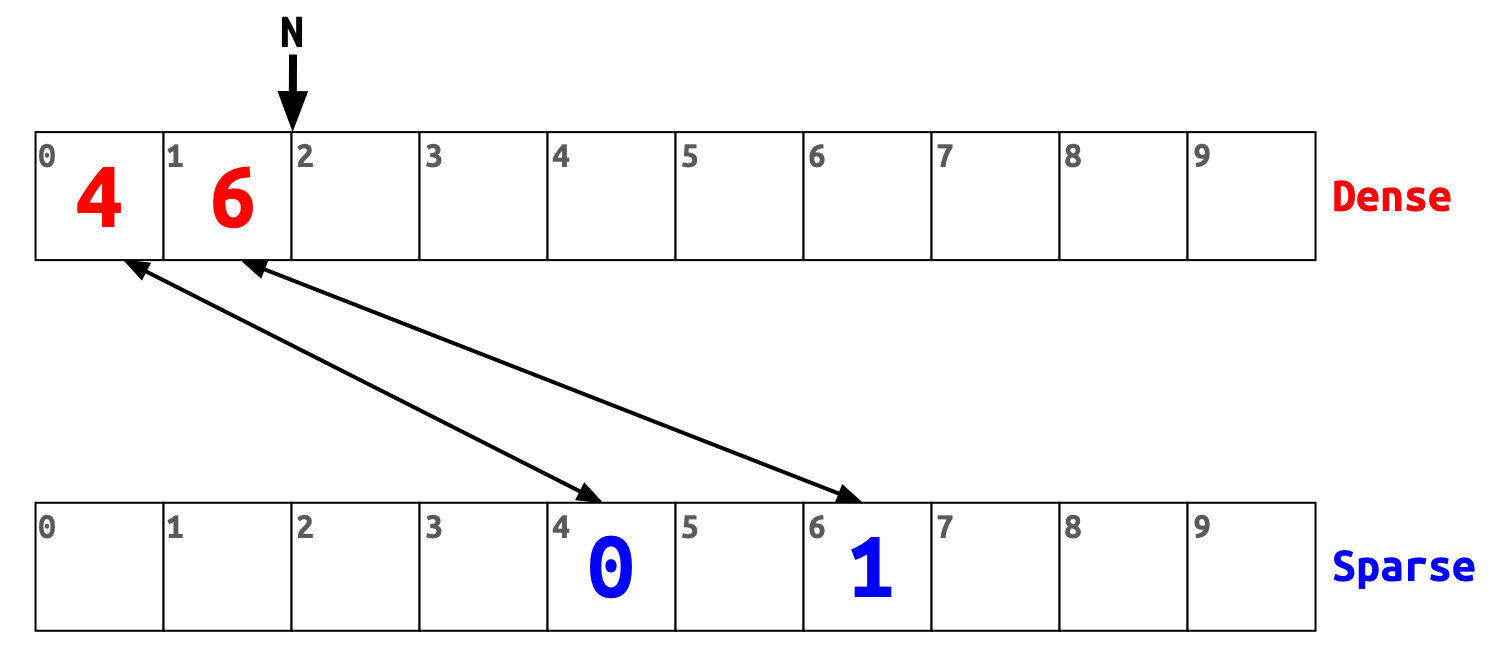
The steps are the same. We put 6 to the next free slot of the dense array, write N to the sparse at index 6, and increase N by one.

The sparse array has holes, while the dense array items are placed next to each other.

Adding a third item

Now we add 0 as a third item.

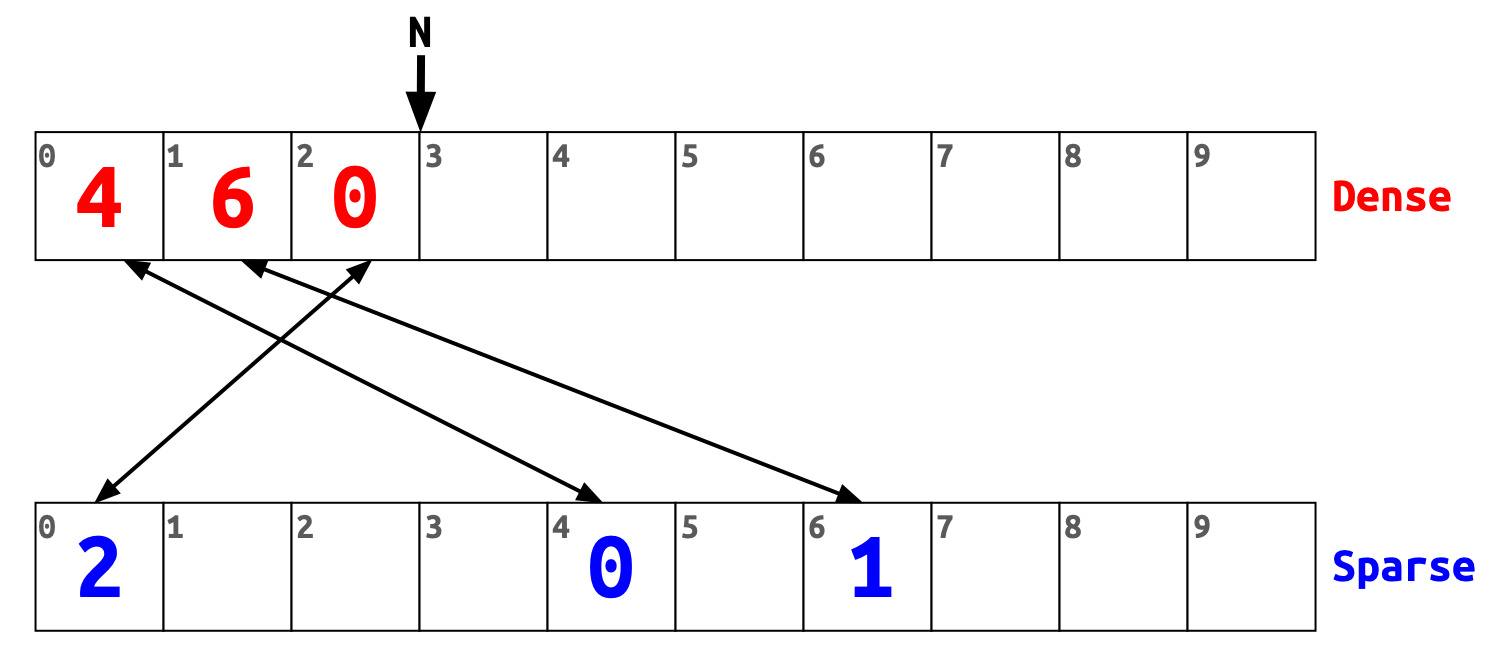
There is nothing new here. The item we added is 0 so we put its dense index (which is 2) to sparse at index 0.

And this is how we can implement it:

void rho_ss_add( struct rho_ss *ss, rho_ss_id id )
{
    assert( ss );
    assert( id <= ss->max );

    if ( rho_ss_has( ss, id ) ) {
        return;
    }

    ss->dense[ss->n] = id;
    ss->sparse[id]   = ss->n;

    ++ss->n;
}

The rho_ss_has function checks if the given item is in the sparse set. We implement it in the next section.

Checking whether an item is in the set

Let’s test if 6 is in the set. To do so we go to the sparse array and check its value at index 6. The value is 1. Now we use this value as an index in the dense array. The dense has value 6 at this index, which means 'yes, the set contains item six'.

Now let’s check if 9 is in the set. We go to the sparse array and check its value at index 9. The value is garbage (we haven’t initialised the memory, remember?) and can be anything, let’s say it is X.

If X >= N then X is out of bounds index for the dense array and 9 is not in the set.

Suppose X is less than N. In our case it should be either of 0, 1, or 2 because N is 3. We check if the dense array’s value at index X is 9. It is not and it cannot be, so the answer is 'no, the set does not contain item nine'.

Now we can implement the operation:

bool rho_ss_has( struct rho_ss *ss, rho_ss_id id )
{
    assert( ss );
    assert( id <= ss->max );

    rho_ss_id dense_index = ss->sparse[id];

    return dense_index < ss->n && ss->dense[dense_index] == id;
}

Removing an item

Let’s remove 6 from the set.

First, we replace 6 with the last item from the dense array, which is 0. Then we have to update the spare array at index 0 with the new index of 0 in the dense array, which is 1. And then reduce N by one.

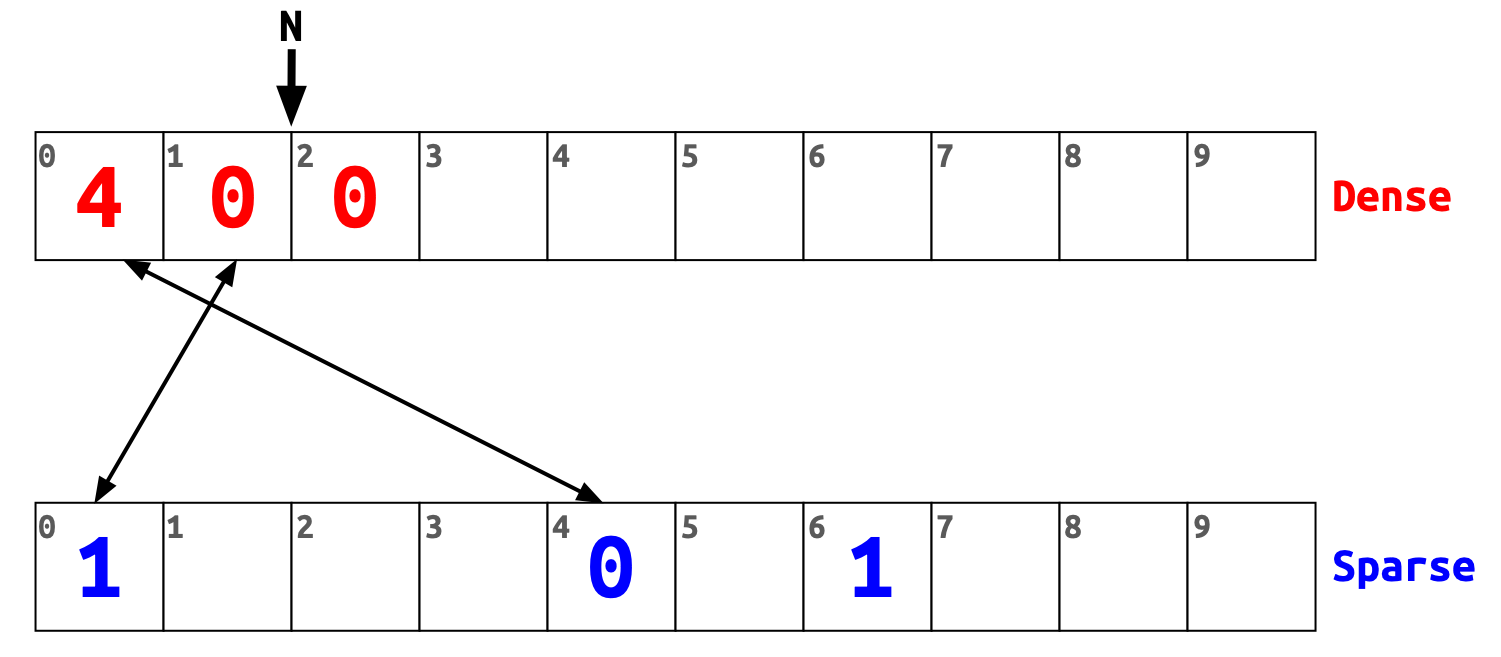
In other words to remove an item from the set, we replace it with the last item in the dense array and update the corresponding sparse array’s slot to point to the new location.

The implementation is as follows:

void rho_ss_remove( struct rho_ss *ss, rho_ss_id id )
{
    assert( ss );
    assert( id <= ss->max );

    if ( rho_ss_has( ss, id ) ) {
        --ss->n;
        rho_ss_id dense_index  = ss->sparse[id];
        rho_ss_id item         = ss->dense[ss->n];
        ss->dense[dense_index] = item;
        ss->sparse[item]       = dense_index;
    }
}

Iterating over the set

This one is super simple. You just iterate over the dense array.

Like this (highlighted lines):

struct rho_ss ss = rho_ss_alloc( 10 );
rho_ss_add( &ss, 4 );
rho_ss_add( &ss, 6 );
rho_ss_add( &ss, 0 );

for ( rho_ss_id i = 0; i < ss.n; ++i ) {
    printf( "%d ", ss.dense[i] );
}
printf( "%s", "\n" );

rho_ss_free( &ss );

Clearing the set

Just set N to zero:

void rho_ss_clear( struct rho_ss *ss )
{
    assert( ss );

    ss->n = 0;
}

Like I said before, most of the sparse set operations are super fast.

What’s next?

You could play with my implementation of the sparse set or (and this is preffered way) implement it on your own.